
Shapes can be put under transformations. This means a shape can be changed by a set of instructions. The original shape is put under instructions which are given to you. You may be able to change a whole shape or transform the shape vertex by vertex. Below are the main types of transformations:
Reflection

A reflection is made with the use of a mirror line. Each vertex of the shape is reflected to the opposite side of the mirror line. The new point is perpendicular to the mirror line and is equal in distance from the mirror line as the original shape is from the mirror line.
Rotation
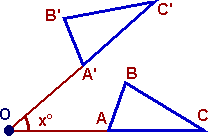
Rotations are made about a centre of rotation. The centre would be given to you or you will have to work backward for it. An angle of rotation is also given to you. A positive rotation goes anti-clockwise and a negative rotation goes clockwise. The rotation is made by connecting a vertex to the centre of rotation and rotating it for the image.
Enlargement

To make an enlargement of a shape you need to have a centre of enlargement. Also, you need a scale factor which tells you the change in size. You find the enlargement of an object by using the veracities. You join a vertex to the centre of enlargement. Measure the length of this line. Multiply this by the scale factor and extend the line to this length. Repeat this with all of the vertices and then join the ends up. A negative enlargement means the image is on the opposite side of the centre of enlargement.
Translation

A translation is given to you in the form:

The x means how many units you should move the shape along the horizontal and the y means how many units it should be translated along the vertical axis. A positive x means moving to the right while a negative x means moving to the left. A positive y means moving up while a negative y means moving down.